方程式を答えから解く！？

電気工事士の筆記試験は、解答方式がマークシートによる四肢択一形式です。 四肢択一ということは、あらかじめ用意されている4個の選択肢の中から1個の正解を選び出すということです。

言い換えれば、正しい答えは4個の選択肢の中にあります。方程式を用いる問題の場合、選択肢の答えを順番に方程式に代入すれば、自ずと答えがわかるはずです。但し、この方法は問題の答えが方程式の解の場合のみ使えます。

問題を解く時間がないときや、どうしても方程式が解けないという場合に必ず役に立ちます。参考までに、例題を解きながら方程式を答えから解く方法を解説したいと思います。

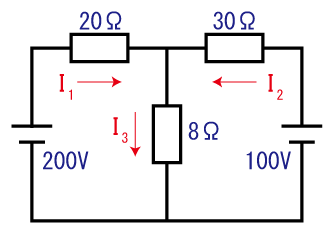
【例題】 左図の回路の8Ωの抵抗を流れる電流I₃はいくらか？正しい電流値を次の中から選べ

• 6A
• 8A
• 10A
• 12A

【解法】
キルヒホッフの第1則より、
I₃ ＝ I₁ ＋ I₂・・・(Ａ)
キルヒホッフの第2則より、
20I₁ ＋ 8I₃ ＝ 200・・・(Ｂ)
30I₂ ＋ 8I₃ ＝ 100・・・(Ｃ)
これから連立方程式を解いて解を求めるわけですが、計算が面倒ですよね！
そこで、選択肢の答えを方程式に代入するわけです。

選択肢の答え(1)6Aを方程式に代入

(Ｃ)式に I₃ ＝ 6 を代入すると、
20I₁ ＋ 8I₃ ＝ 200
I₁ ＝ (200 − 8I₃) ／ 20 ＝ (200 − 8 × 6) ／ 20 ＝ 7.6
(Ａ)式より、I₃ ＝ I₁ ＋ I₂ なので、
I₂ ＝ I₃ − I₁ ＝ 6 − 7.6 = −1.6
(Ｃ)式 30I₂ ＋ 8I₃ ＝ 100 に I₂ ＝ −1.6、I₃ ＝ 6 を代入すると、
30I₂ ＋ 8I₃ ＝ 30 × (-1.6) ＋ 8 × 6 ≠ 100
よって答えは 6A ではない。

選択肢の答え(2)8Aを方程式に代入

(Ｂ)式に I₃ ＝ 8 を代入すると、
20I₁ ＋ 8I₃ ＝ 200
I₁ ＝ (200 − 8I₃) ／ 20 ＝ (200 − 8 × 8) ／ 20 ＝ 6.8
Ａ式より I₃ ＝ I₁ ＋ I₂ なので、
I₂ ＝ I₃ − I₁ ＝ 8 − 6.8 = 1.2
(Ｃ)式 30I₂ ＋ 8I₃ ＝ 100 に I₂ ＝ 1.2、_I3 ＝ 8 を代入すると、
30I₂ ＋ 8I₃ ＝ 30 × 1.2 ＋ 8 × 8 ＝ 100
となり、(2)の 8A が答えとなるのです。

• 「筆記試験の受験アドバイス」に戻る